Le 9 juillet 1595, Kepler dessinait une figure au tableau noir, dans sa classe, lorsqu’une idée le frappa soudain avec tant de force qu’il crut détenir la clef des secrets de la création.– “La joie que me donna ma découverte, je ne pourrai jamais la dire.”
Il élabora un modèle cosmique où les cinq solides réguliers déterminaient l’agencement des six planètes.
– “ Je réussis à les ranger si heureusement que, plus tard, quand je vérifiai ces dispositions, je n’eus rien à y changer. Je ne regrettais plus alors le temps perdu ; je n’étais plus las de mon travail ; je ne reculais devant aucun calcul, si difficile qu’il fût. Jour et nuit je fis mes calculs pour voir si la proposition que je venais de formuler s’accordait avec les orbites de Copernic.”
Mais son modèle ne s’accorde pas avec les données de Copernic, les données astronomiques disponibles à l’époque. La faute devait être soit à son modèle, soit aux données de Copernic ; naturellement Kepler préféra blâmer ces dernières. Il lui fallait donc des données plus exactes. Il savait où les trouver… Chez Tycho Brahe, noble danois irascible, grand observateur du ciel.
– “Gardons tous le silence, écoutons Tycho qui a consacré trente-cinq ans à ses observations… Je n’attends que Tycho ; il m’expliquera l’ordre et l’arrangement des orbites… alors j’espère, un jour, si Dieu me prête vie, ériger un admirable édifice. N’importe lequel de ses instruments vaut plus que ma fortune et celle de toute ma famille ensemble… Voici ce que je pense de Tycho : il est superlativement riche, mais il ne sait pas se servir de ce qu’il a, comme c’est le cas de la plupart des riches. Donc il faut essayer de lui dérober ses richesses.”
Quand il arriva à l’observatoire de Tycho Brahe, Kepler reçut en partage l’étude de Mars, notoirement la plus difficile planète. Kepler, fier d’être chargé de Mars, se vanta de résoudre en huit jours le problème de l’orbite, et fit même un pari à ce sujet. Les huit jours se changèrent en huit ans.
– “Mars est le puissant vainqueur de la curiosité humaine, qui a bafoué tous les stratagèmes des astronomes, ruiné leurs outils, défait leurs armées ; ainsi a-t-il assuré le secret de son règne à travers tous les siècles passés et poursuit-il sa course dans une liberté sans frein. Mars est un astre qui défie l’observation.”
Kepler fit une première hypothèse selon laquelle l’orbite de Mars serait circulaire, et chercha à la faire concorder avec les observations de Tycho Brahe, à force de calculs. Voici ce qu’il nous dit entre deux pages de calcul :
– “Si tu es las de cette fatigante méthode de calcul, prends pitié de moi qui dus y passer en recommençant au moins soixante-dix fois à très grande perte de temps ; et tu ne seras pas surpris d’apprendre qu’il y a presque cinq ans passés que je m’attaquai à Mars.”
Il y parvint… presque : entre les positions observées et les positions que Mars aurait dû occuper selon sa théorie il y avait jusqu’à huit minutes d’écart. Kepler se montra humble devant ces huit minutes.
– “La divine bonté nous a donné en Tycho un observateur si fidèle que nous devons reconnaître ce don divin et nous en servir… Désormais j’avancerai vers ce but selon mes idées. Car si j’avais cru pouvoir ignorer ces huit minutes, j’aurais accomodé comme il convenait mon hypothèse. Mais il n’était pas permis de les ignorer et ces huit minutes montrent la voie d’une réforme complète de l’Astronomie.”
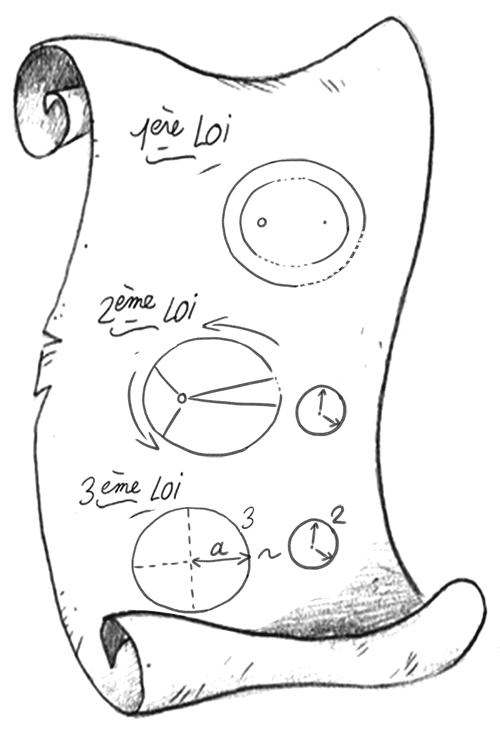
Pour déterminer précisément la trajectoire de Mars à partir des observations, il fallait connaître précisément le mouvement de la Terre, et c’est ce qui amena Kepler à découvrir sa Deuxième Loi avant sa Première loi. Puis il retourna à l’assaut de Mars, à qui il essaya une dernière fois d’attribuer une orbite circulaire, en vain.
– “La conclusion est tout simplement que le trajet de la planète n’est pas un cercle —il s’incurve des deux côtés et s’étale aux autres bouts. Cette courbe s’appelle une ovale. L’orbite n’est pas un cercle, mais une figure ovale.”
Il tâtonna pour déterminer précisément cette courbe ovale, se perdant dans de fausses conjectures et d’interminables calculs. A propos de l’une de ces fausses conjectures :
– “Ce qui m’est arrivé confirme le proverbe : une chienne trop pressée fait des chiots aveugles… Je ne pouvais pas imaginer d’autre moyen d’imposer un cours ovale aux planètes. Quand ces idées me vinrent j’avais déjà célébré mon nouveau triomphe sur Mars sans être troublé par la question…de savoir si les chiffres s’accordaient ou non… Ainsi me fourrai-je dans un nouveau labyrinthe… Le lecteur doit faire preuve de tolérance pour ma crédulité.”
Finalement la lumière lui creva les yeux. La forme elliptique des trajectoires devenait une solution évidente, mais il ne la voyait pas.
– “Si seulement la forme était une ellipse parfaite, on trouverait toutes le réponses dans Archimède et dans Apollonius.”
18 mois plus tard :
– “La vérité doit se trouver à mi-chemin entre l’ovale et le cercle, exactement comme si l’orbite de Mars était une ellipse parfaite. Mais à cet égard je n’ai encore rien exploré.“
Finalement, le déclic se fit, à l’occasion d’une coïncidence numérique qui n’en était pas une. Après toutes ces années, Kepler avait l’esprit si bien saturé de données numériques sur l’orbite de Mars qu’au premier hasard il réagit immédiatement comme un nuage chargé d’électricité réagit à une étincelle, et découvrit l’équation de l’orbite de Mars… sans comprendre que c’était l’équation d’une ellipse. Mais comme il n’arrivait pas à tracer la courbe vérifiant cette équation, il tenta une dernière hypothèse, qu’il pensait être différente mais qui était en fait la même : celle d’une trajectoire elliptique. Alors il se rendit compte que les deux méthodes donnaient le même résultat :
– “ Pourquoi mâcher mes mots ? La vérité de la Nature, que j’avais repoussée et chassée, revint en tapinois par la petite porte en se déguisant pour se faire accepter. C’est-à-dire, je mis de côté l’équation originale et retombai sur les ellipses, croyant que c’était une hypothèse différente, alors que les deux sont une seule et même chose… Je faillis devenir fou à chercher une raison expliquant pourquoi la planète préférait une orbite elliptique… Ah ! quel étourneau j’ai été !”