L’ellipse est un des objets que tous les mathématiciens ont dans leur boîte à outils. Nous aimons vraiment bien les ellipses ! Et les planètes, qui suivent des trajectoires elliptiques, les aiment bien aussi.
Vive l’ellipse !
Une forme simple qu'on retrouve dans les maths et dans le cielC’est joli !
Les planètes tournent autour de leurs étoiles selon une ellipse.
Mais si on ne sait pas ce que c’est, ça ne nous avance pas bien loin.
Essayons donc d’en construire une, suivant l’exemple de cet homme qui essaye de déformer son cercle tant qu’il peut. Pour obtenir une ellipse, et n’importe laquelle, c’est comme cela qu’il faut faire : prendre un cercle parfait et le contracter ou le dilater selon une des deux directions principales ! On obtient un cercle aplati, qui n’est pas un ovale, mais une forme géométrique importante pour les mathématiciens.
Mais c’est quoi ?
Une courbe
Une ellipse est une courbe plane : un objet qu’on peut tracer au crayon sur une feuille de papier.
Des foyers
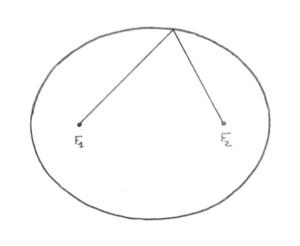
Il y a deux points importants dans l’intérieur d’une ellipse : ce sont ses foyers. Sur le dessin ce sont F1 et F2.
Pour tous les points de l’ellipse, la distance au premier foyer ajoutée à la distance au deuxième foyer est la même ; c’est comme ça qu’on peut la construire.
Un centre et deux symétries
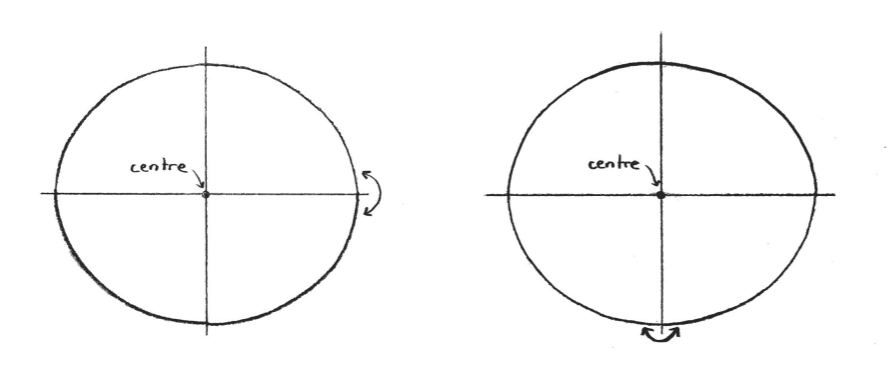
Le centre de l’ellipse est le milieu des deux foyers. Une ellipse est toujours symétrique par rapport à la droite définie par les deux foyers, mais aussi par la perpendiculaire à cette droite qui passe par le centre. Ça a l’air compliqué, mais ça se voit bien avec une figure !
Une équation
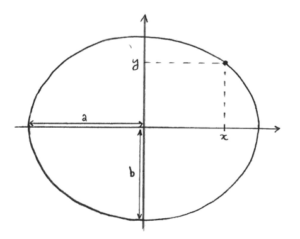
Que ferait un mathématicien sans équation ? Celle de l’ellipse est :
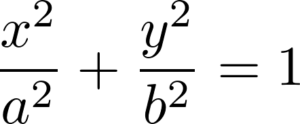
Ça veut dire que si on repère les points du plan par leurs coordonnées (x,y), avec x en abscisse et y en ordonnée, alors les points de l’ellipse vérifient l’équation donnée. Mais alors c’est quoi ce a et ce b ? Ce sont des paramètres choisis à notre bon vouloir. Si on les change, notre ellipse va changer ! Quand a=b, on obtient un cercle, qui est un cas particulier d’ellipse.
Est-ce une ellipse ?!
La portion de champ broutée par une chèvre attachée à deux poteaux par une corde coulissante
oui
Bravo !
C’est la manière la plus simple de dessiner une ellipse, avec un crayon, du fil et deux épingles.
non
Et si !
C’est la manière la plus simple de dessiner une ellipse, avec un crayon, du fil et deux épingles.
Ce que trace un compas (un cercle quoi)
oui
Le cercle est bien une ellipse ! C’en est une un peu dégénérée, sans vouloir offenser ce pauvre cercle, dont les deux foyers sont confondus sur le centre du cercle
non
Ce non est bien compréhensible, mais c’est en fait un oui. Ce fourbe de cercle est une ellipse cachée –dégénérée diront les mathématiciens– dont les deux foyers sont confondus sur le centre.
La trajectoire d’une planète autour de son étoile
oui
Bien sûr ! C’est un astronome allemand, Johannes Kepler, qui a trouvé cela au XVIeme siècle. Ce n’était pas une mince affaire ; ça lui a quand même pris 7 ans, à partir des observations de Mars.
(en fait, ce n’est pas e-xac-te-ment une ellipse, à cause des l’influence des autre planètes, mais presque !)
non
Allons, allons, ressaisissez-vous ! S’il y a une chose à retenir c’est bien celle-là : les planètes tournent autour de leur étoile selon une ellipse. Bon, on a qu’à dire que ça va pour cette fois.
(en fait, ce n’est pas e-xac-te-ment une ellipse, à cause des l’influence des autre planètes, mais presque !)
Un anneau vu de trois quarts
oui
Oui, tout comme les assiettes vus de trois quarts, les cercles dessinés en perspective, etc. En fait, on voit des ellipses à longueur de journée…
non
Si ! Tout comme les assiettes vus de trois quarts, les cercles dessinés en perspective, etc. En fait, on voit des ellipses à longueur de journée…
Une tranche de cylindre
oui
Effectivement ! Tout comme pour le cône, une tranche de cylindre est une ellipse. Les mathématiciens diront même qu’un cylindre n’est rien de moins qu’un cône dont la pointe est située… à l’infini.
non
Et bien si, c’en est bien une. Tout comme pour le cône, une tranche de cylindre est une ellipse. Les mathématiciens diront même qu’un cylindre n’est rien de moins qu’un cône dont la pointe est située… à l’infini.
Les maths dans la vie
Il n’est pas rare que les objets mathématiques soient repris dans la culture littéraire, voire même dans le langage courant. Après tout, ces objets si abstraits peuvent livrer de nouvelles manières pour décrire les choses de la vie, les tréfonds du monde et de l’âme, tant l’interprétation qu’on peut en faire peut être vaste. Ce n’est pas Victor Hugo qui dira la contraire, utilisant l’image de l’ellipse en 1862 dans Les Misérables :
”L'homme n'est pas un cercle à un seul centre ; c'est une ellipse à deux foyers. Les faits sont l'un, les idées l'autre.
L’ellipse a aussi son sens propre en littérature. C’est une figure de style où l’auteur omet quelques mots.
Les définitions littéraires et géométriques de l’ellipse sont toutes les deux liées par l’étymologie. En grec ancien, ἔλλειψις signifie manque : il manque des mots quand on est en face d’une ellipse littéraire, on manque de peu d’être un cercle quand prend place la géométrie.
Pour continuer à regarder la vie quotidienne à travers le prisme des mathématiques
Le chaos se cache un peu
Notre système solaire a l’air bien calme, pour un système chaotique
Tout savoir sur l’ellipse :
- À l’aide du merveilleux site Mathcurve, et de sa très complète description de l’ellipse. Vous pourrez également y découvrir la famille des coniques, à laquelle appartient l’ellipse, ainsi que la cardioïde et les courbes dessinées par un spirographe, évoquées dans le quizz.
- Sur la page wikipédia dédiée.
La citation de Victor Hugo est issue du roman Les Misérables, tome IV, livre 7. Consultable sur wikisource.